Luigi Guido Grandi acreditava ter encontrado a prova matemática da Criação ao resolver uma série infinita, relacionada à Quadratura do Círculo.
A Matemática é uma ferramenta poderosa que pode ser usada para explicar fenômenos complexos e entender o mundo ao nosso redor. Embora seja difícil determinar se a Matemática pode explicar o significado da vida, do universo e de tudo o mais, é inegável que ela desempenha um papel fundamental em nossa compreensão do cosmos. Uma das áreas da Matemática que pode nos ajudar a entender melhor o universo é o Cálculo, que estuda as taxas de mudança e a acumulação de quantidades.
Outra área importante da Matemática é a Geometria, que se concentra no estudo das formas e figuras geométricas. Juntamente com a Álgebra, que lida com a resolução de equações e manipulação de expressões, essas áreas da Matemática podem ser usadas para modelar e analisar fenômenos complexos, como o início do universo. Embora a Matemática possa não ser capaz de explicar tudo, é uma ferramenta valiosa para entender o mundo e o universo. A busca por respostas é um desafio contínuo.
A Matemática e a Série de Grandi
A Matemática é uma disciplina que tem fascinado os seres humanos por séculos. Uma das questões mais intrigantes é a série infinita de 1 − 1 + 1 − 1 +…, que tem ocupado os maiores matemáticos desde o século 18. A pergunta é: qual é o resultado dessa soma infinita? Uma resposta intuitiva é que não há resposta, pois a soma se altera entre 0 e 1 sem nunca chegar a um valor único. No entanto, essa é apenas uma das quatro opções consideradas ao longo do tempo.
A série de Grandi é um exemplo clássico de uma soma infinita que tem sido estudada por matemáticos ao longo da história. O matemático italiano Luigi Guido Grandi (1671 – 1742) foi um dos primeiros a chamar a atenção para essa série. Grandi foi um padre, filósofo, matemático e engenheiro que nasceu em Cremona, na Itália. Seu interesse pela Matemática demorou a surgir, mas com seu primeiro livro, ‘Geometrica divinatio Vivianeorum problematum’, publicado em 1699, ele ganhou reconhecimento em seu país e em outros.
A Contribuição de Grandi para a Matemática
Grandi foi um matemático prolífico que contribuiu significativamente para a Matemática. Ele foi responsável por importantes projetos de engenharia, incluindo a drenagem do Vale de Chianna. Além disso, ele colaborou na publicação da primeira edição das obras de Galileu Galilei (1718) e publicou uma versão italiana dos ‘Elementos’ de Euclides (1731). Grandi também aconselhou o Papa Clemente sobre a reforma do calendário e introduziu na Itália as ideias de Gottfried Leibniz sobre Cálculo.
Uma de suas obras mais admiradas foi o estudo da rosa polar, uma família de curvas que lembram flores, que chamou de rhodoneas (do grego rhodon, rosa), em seu livro ‘Flores Geometrici’ (1725). No entanto, foi sua obra ‘Quadratura do Círculo e da Hipérbole’, publicada em 1703, que despertou uma acalorada polêmica em torno da série que leva seu nome.
A Série de Grandi e a Controvérsia
A série de Grandi é uma soma infinita de 1 − 1 + 1 − 1 +…, que pode ser representada de diferentes maneiras. Grandi estudou essa soma e observou que, adicionando parênteses, chegava-se a resultados diferentes. Por exemplo, (1 – 1) + (1 – 1) + (1 – 1)… resulta em 0 + 0 + 0…, que é igual a 0. No entanto, se fosse escrito assim: 1 + (- 1 + 1) + (- 1 + 1) + (- 1 + 1)…, a soma seria 1 + 0 + 0 + 0…, o que daria 1.
Grandi afirmou que a soma de infinitos 0s é igual a 1/2, o que foi considerado surpreendente. Ele preferiu explicar esse resultado com uma parábola em que imaginava dois irmãos que herdaram dos pais uma joia valiosa. Eles foram proibidos de vendê-la e dividi-la à metade destruiria seu valor. Os irmãos concordaram que alternariam a propriedade da joia, o que leva a uma série infinita de 1 − 1 + 1 − 1 +…. Grandi argumentou que a soma dessa série é igual a 1/2, o que é o valor da joia.
A série de Grandi é um exemplo clássico de uma soma infinita que tem sido estudada por matemáticos ao longo da história. A controvérsia em torno dessa série é um exemplo da complexidade e da beleza da Matemática, que continua a fascinar os seres humanos até hoje.
Fonte: © G1 – Globo Mundo

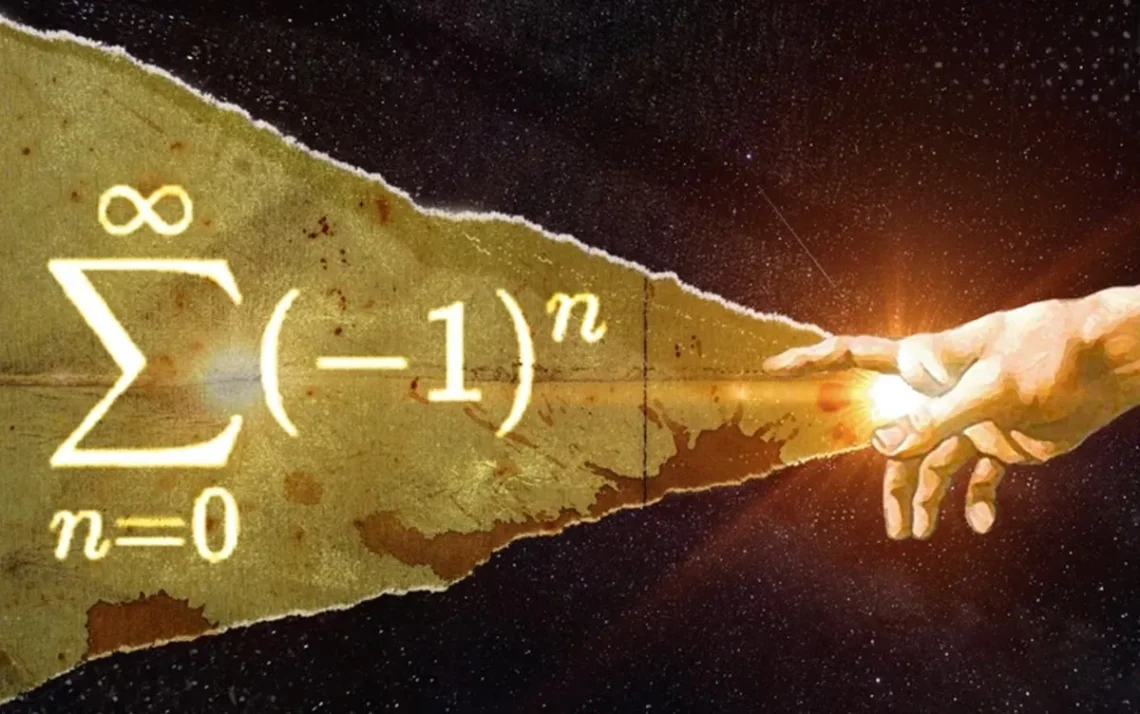






Comentários sobre este artigo